Is it on a GeoRegion Boundary?

Sometimes, we don't just want information on whether a point is inside a GeoRegion. Sometimes, it is important to know if something is on the boundary of a GeoRegion. This would prove useful in determining if the shapes of two different GeoRegions are equivalent to each other.

Point2 Type

We use the Point2 Type from the package GeometryBasics.jl, which is reexported by GeoRegions.jl, as an easy way to denote points. This also allows us to use the package GeometryOps.jl to determine if a point is on a GeoRegion boundary.

using GeoRegions
using DelimitedFiles
import CairoMakie: Figure, Axis, lines!, scatter!, resize_to_layout!

download("https://raw.githubusercontent.com/natgeo-wong/GeoPlottingData/main/coastline_resl.txt","coast.cst")
coast = readdlm("coast.cst",comments=true)
clon  = coast[:,1]
clat  = coast[:,2]
nothing

Is a Point on a GeoRegion Boundary?

As an example, let us test if a point is on the perimeter of the GeoRegion AR6_EAO, defined in the blue bounding box below.

geo = GeoRegion("AR6_EAO")

The GeoRegion AR6_EAO has the following properties:
    Region ID     (ID) : AR6_EAO
    Parent ID    (pID) : GLB
    Name        (name) : Equatorial Atlantic Ocean
    Bounds   (N,S,E,W) : 7.6, -10.0, 8.0, -50.0
    Rotation       (θ) : 0.0
    File Path   (path) : /home/runner/work/GeoRegions.jl/GeoRegions.jl/src/.files/AR6/AR6_EAO.json
    Centroid (geometry.centroid) : [-19.31990102509721, -1.27790738776953]
    Shape       (geometry.shape) : Vector{Point{2, Float64}}(8)

Next, we select a point along the border

A = Point(-25,7.6)
B = Point(335,7.6)
C = Point(-20,5)
D = Point(-45,-7.5)

2-element Point{2, Float64} with indices SOneTo(2):
 -45.0
  -7.5

Here, we note that A and B

slon,slat = coordinates(geo)
aspect = (maximum(slon)-minimum(slon))/(maximum(slat)-minimum(slat))
fig = Figure()
ax = Axis(
    fig[1,1],width=750,height=750/aspect,
    limits=(minimum(slon)-2,maximum(slon)+2,minimum(slat)-2,maximum(slat)+2),
    xlabel = "Longitude / º", ylabel = "Latitude / º"
)
lines!(ax,clon,clat,color=:black,linewidth=3)
lines!(ax,slon,slat,linewidth=5)
scatter!(ax,A,markersize=20)
scatter!(ax,C,markersize=20)
scatter!(ax,D,markersize=20)
resize_to_layout!(fig)
fig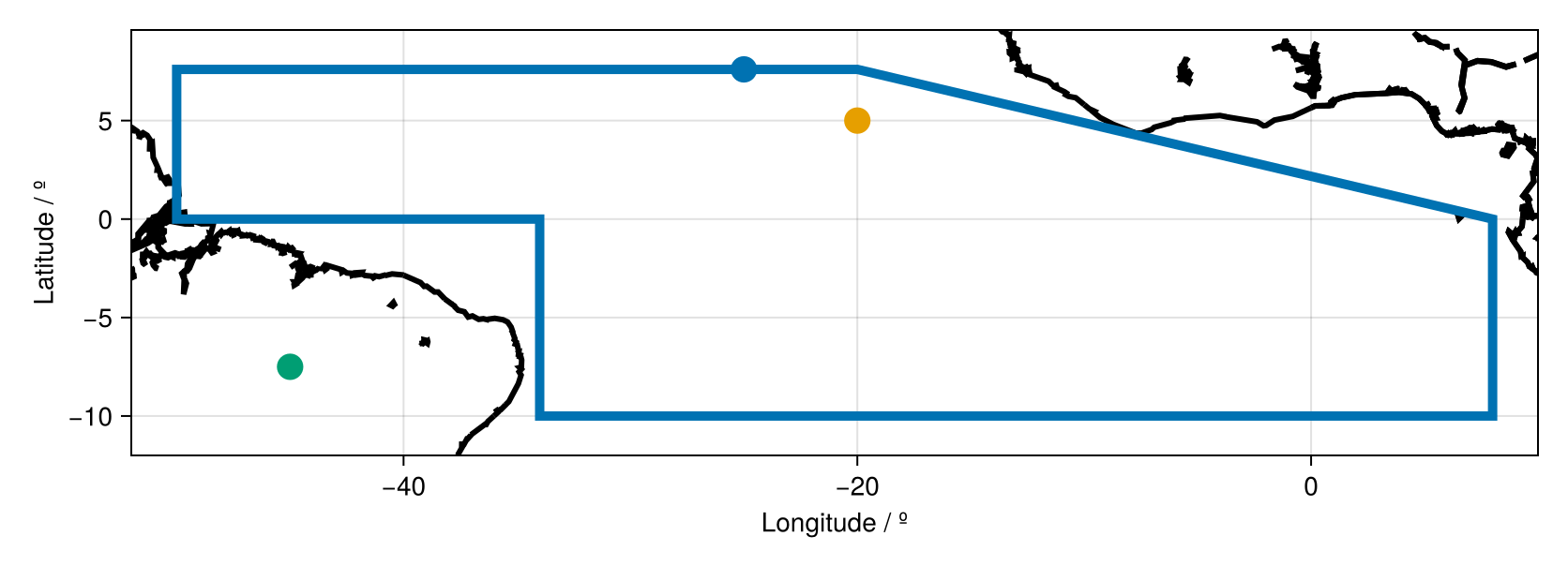

By eye it is easy to see that Point A is on the GeoRegion perimeter. However, C and D are not. Let us now see if we are able to corroborate this with GeoRegions.jl using the function on()

on(A,geo), # Point A
on(C,geo), # Point C
on(D,geo)  # Point D

(true, false, false)

But what about Point B? Point B is also very obviously on the bounds of the GeoRegion, it is simply that the longitude of Point B is shifted by 360º from A such that it is now in the (0,360) coordinates frame. We see that this is of no concern to GeoRegions.jl, which can detect that it is within the bounds of the GeoRegion anyway.

on(B,geo)

true

See the API here

Is a GeoRegion on a GeoRegion? (i.e., Are their Shapes the Same?)

We can also use the on() function to determine if the perimeter of a GeoRegion is on the perimeter of another. Or, in simpler terms, if two GeoRegions define the same shape. For example:

on(geo,geo)

true

See the API here

Which is obvious because we are comparing a GeoRegion against itself. However, let us try something a bit more complicated.

1. circshift() the points defining the GeoRegion

In this test case, we use circshift() to change the starting and ending coordinates of the shape. Therefore, we are defining the same region, just with different start and ending points.

lon,lat = coordinates(geo)
pop!(lon); lon = circshift(lon,2); lon = vcat(lon,lon[1])
pop!(lat); lat = circshift(lat,2); lat = vcat(lat,lat[1])
geo2 = GeoRegion(lon,lat)

The GeoRegion  has the following properties:
    Region ID     (ID) : 
    Parent ID    (pID) : 
    Name        (name) : 
    Bounds   (N,S,E,W) : 7.6, -10.0, 8.0, -50.0
    Rotation       (θ) : 0.0
    File Path   (path) : /home/runner/.georegions/.json
    Centroid (geometry.centroid) : [-19.31990102509721, -1.27790738776953]
    Shape       (geometry.shape) : Vector{Point{2, Float64}}(8)

So here, we have circshifted the lon and lat values used to define the GeoRegion such that instead of the start/end points being at (-34,-10), now the start/end points are at (-50,0).

We compare the shapes of the two GeoRegions:

on(geo,geo2),
on(geo2,geo)

(true, true)

And see that the GeoRegions define the same area.

Order of GeoRegions does not matter in on()

The order should not matter, because in the on() function, the GeoRegions are both compared against each other. So on(geo,geo2) = on(geo2,geo). If you find any edge cases where this is not the case, please let me know and I will look into it.

2. Shifting the GeoRegion by 360º

In this test case, we shift the lon of a given GeoRegion by 360º, so that it is on a (0,360) grid instead of a (-180,180) grid.

geo3 = GeoRegion("AR6_WNA")

The GeoRegion AR6_WNA has the following properties:
    Region ID     (ID) : AR6_WNA
    Parent ID    (pID) : GLB
    Name        (name) : Western North America
    Bounds   (N,S,E,W) : 50.0, 33.8, -105.0, -130.0
    Rotation       (θ) : 0.0
    File Path   (path) : /home/runner/work/GeoRegions.jl/GeoRegions.jl/src/.files/AR6/AR6_WNA.json
    Centroid (geometry.centroid) : [-115.7352941176471, 42.376470588235314]
    Shape       (geometry.shape) : Vector{Point{2, Float64}}(5)

In this case, the longitude is all <0º, so we can simply add 360º to the longitude and transform it from a 180ºW-180ºE grid to a 0º-360ºE grid.

lon,lat = coordinates(geo3); lon = lon .+ 360
geo4 = GeoRegion(lon,lat)

The GeoRegion  has the following properties:
    Region ID     (ID) : 
    Parent ID    (pID) : 
    Name        (name) : 
    Bounds   (N,S,E,W) : 50.0, 33.8, 255.0, 230.0
    Rotation       (θ) : 0.0
    File Path   (path) : /home/runner/.georegions/.json
    Centroid (geometry.centroid) : [244.26470588235313, 42.376470588235335]
    Shape       (geometry.shape) : Vector{Point{2, Float64}}(5)

We compare the shapes of the two GeoRegions:

on(geo3,geo4)

true

And we see that the GeoRegions define the same area.