Generalized Grids for Data Extraction

Not all longitude-latitude grids are rectilinear in the lon/lat space. RegionGrid classifies this type as a GeneralizedGrid. Examples of such datasets include:

Level 2 products from the Global Precipitation Measurement Mission
Model output from climate models such as Weather Research & Forecasting Model (WRF)

Basically, for each of these datasets, the data is given in such a way that the coordinates of the grid can be expressed via:

A 2D array of Point2 types, with each Point2 type containing (lon,lat)

julia

using GeoRegions
using RegionGrids
using CairoMakie

Creating Generalized Grids

A Generalized Grid can be created as follows:

ggrd = RegionGrid(geo,Point2.(lon,lat))

where geo is a GeoRegion of interest that is found within the domain defined by the longitude and latitude grid vectors.

julia

nlon = 51; nlat = 31
lon = zeros(nlon,nlat)
lat = zeros(nlon,nlat)
for ilat = 1 : nlat, ilon = 1 : nlon
    lon[ilon,ilat] = (ilon-26) * (5 + (ilat-16) * 0.1)
    lat[ilon,ilat] = (ilat-16) * 5
end
geo = GeoRegion([10,100,-80,10],[50,10,-40,50])

ggrd = RegionGrid(geo,Point2.(lon,lat))

The GeneralMask type has the following properties:
    Longitude Indices     (ilon)
    Latitude Indices      (ilat)
    Longitude Points       (lon)
    Latitude Points        (lat)
    Rotated X Coordinates    (X)
    Rotated Y Coordinates    (Y)
    Rotation (°)             (θ) : 0.0
    RegionGrid Mask       (mask)
    RegionGrid Weights (weights)
    RegionGrid Size 	          : 37 lon points x 17 lat points
    RegionGrid Validity          : 230 / 629

The API for creating a Generalized Grid can be found here

What is in a Generalized Grid?

RegionGrids.GeneralizedGrid Type

julia

GeneralizedGrid <: RegionGrid

A GeneralizedGrid is a RegionGrid that is created based on longitude/latitude grids that are not rectilinear - this can range from curvilinear grids to unstructured grids. It has its own subtypes: RegionMask and VectorMask.

All GeneralizedGrid type will contain the following fields:

lon - A Matrix of Floats, defining the longitudes for each point in the RegionGrid that describe the region.
lat - A Matrix of Floats, defining the latitude for each point in the RegionGrid that describe the region.
ilon - A Matrix of Ints, defining the indices used to extract the longitude vector from the input longitude vector.
ilat - A Matrix of Ints, defining the indices used to extract the latitude vector from the input latitude vector.
mask - An Matrix of NaNs and 1s, defining the gridpoints in the RegionGrid where the data is valid.
weights - A Matrix of Floats, defining the latitude-weights of each valid point in the grid. Will be NaN if outside the bounds of the GeoRegion used to define this RectilinearGrid.
X - A Matrix of Floats, defining the X-coordinates (in meters) of each point in the "derotated" RegionGrid about the centroid for the shape of the GeoRegion.
Y - A Matrix of Floats, defining the Y-coordinates (in meters) of each point in the "derotated" RegionGrid about the centroid for the shape of the GeoRegion.
θ - A Float storing the information on the angle (in degrees) about which the data was rotated in the anti-clockwise direction. Mathematically, it is rotation - geo.θ.

source

We see that in a GeneralizedGrid type, we have the lon and lat arrays that defined the longitude and latitude points that have been cropped to fit the GeoRegion bounds.

julia

ggrd.lon

37×17 Matrix{Float64}:
 -73.1  -74.8  -76.5  -78.2  -79.9  …  266.5  264.8  263.1  261.4  259.7
 -68.8  -70.4  -72.0  -73.6  -75.2     272.0  270.4  268.8  267.2  265.6
 -64.5  -66.0  -67.5  -69.0  -70.5     277.5  276.0  274.5  273.0  271.5
 -60.2  -61.6  -63.0  -64.4  -65.8     -77.0  -78.4  -79.8  278.8  277.4
 -55.9  -57.2  -58.5  -59.8  -61.1     -71.5  -72.8  -74.1  -75.4  -76.7
 -51.6  -52.8  -54.0  -55.2  -56.4  …  -66.0  -67.2  -68.4  -69.6  -70.8
 -47.3  -48.4  -49.5  -50.6  -51.7     -60.5  -61.6  -62.7  -63.8  -64.9
 -43.0  -44.0  -45.0  -46.0  -47.0     -55.0  -56.0  -57.0  -58.0  -59.0
 -38.7  -39.6  -40.5  -41.4  -42.3     -49.5  -50.4  -51.3  -52.2  -53.1
 -34.4  -35.2  -36.0  -36.8  -37.6     -44.0  -44.8  -45.6  -46.4  -47.2
   ⋮                                ⋱                         ⋮    
  47.3   48.4   49.5   50.6   51.7      60.5   61.6   62.7   63.8   64.9
  51.6   52.8   54.0   55.2   56.4      66.0   67.2   68.4   69.6   70.8
  55.9   57.2   58.5   59.8   61.1  …   71.5   72.8   74.1   75.4   76.7
  60.2   61.6   63.0   64.4   65.8      77.0   78.4   79.8   81.2   82.6
  64.5   66.0   67.5   69.0   70.5      82.5   84.0   85.5   87.0   88.5
  68.8   70.4   72.0   73.6   75.2      88.0   89.6   91.2   92.8   94.4
  73.1   74.8   76.5   78.2   79.9      93.5   95.2   96.9   98.6  100.3
  77.4   79.2   81.0   82.8   84.6  …   99.0  100.8  102.6  104.4  106.2
  81.7   83.6   85.5   87.4   89.3     104.5  106.4  108.3  110.2  112.1

julia

ggrd.lat

37×17 Matrix{Float64}:
 -35.0  -30.0  -25.0  -20.0  -15.0  …  20.0  25.0  30.0  35.0  40.0  45.0
 -35.0  -30.0  -25.0  -20.0  -15.0     20.0  25.0  30.0  35.0  40.0  45.0
 -35.0  -30.0  -25.0  -20.0  -15.0     20.0  25.0  30.0  35.0  40.0  45.0
 -35.0  -30.0  -25.0  -20.0  -15.0     20.0  25.0  30.0  35.0  40.0  45.0
 -35.0  -30.0  -25.0  -20.0  -15.0     20.0  25.0  30.0  35.0  40.0  45.0
 -35.0  -30.0  -25.0  -20.0  -15.0  …  20.0  25.0  30.0  35.0  40.0  45.0
 -35.0  -30.0  -25.0  -20.0  -15.0     20.0  25.0  30.0  35.0  40.0  45.0
 -35.0  -30.0  -25.0  -20.0  -15.0     20.0  25.0  30.0  35.0  40.0  45.0
 -35.0  -30.0  -25.0  -20.0  -15.0     20.0  25.0  30.0  35.0  40.0  45.0
 -35.0  -30.0  -25.0  -20.0  -15.0     20.0  25.0  30.0  35.0  40.0  45.0
   ⋮                                ⋱                           ⋮    
 -35.0  -30.0  -25.0  -20.0  -15.0     20.0  25.0  30.0  35.0  40.0  45.0
 -35.0  -30.0  -25.0  -20.0  -15.0     20.0  25.0  30.0  35.0  40.0  45.0
 -35.0  -30.0  -25.0  -20.0  -15.0  …  20.0  25.0  30.0  35.0  40.0  45.0
 -35.0  -30.0  -25.0  -20.0  -15.0     20.0  25.0  30.0  35.0  40.0  45.0
 -35.0  -30.0  -25.0  -20.0  -15.0     20.0  25.0  30.0  35.0  40.0  45.0
 -35.0  -30.0  -25.0  -20.0  -15.0     20.0  25.0  30.0  35.0  40.0  45.0
 -35.0  -30.0  -25.0  -20.0  -15.0     20.0  25.0  30.0  35.0  40.0  45.0
 -35.0  -30.0  -25.0  -20.0  -15.0  …  20.0  25.0  30.0  35.0  40.0  45.0
 -35.0  -30.0  -25.0  -20.0  -15.0     20.0  25.0  30.0  35.0  40.0  45.0

An example of using Generalized Grids

Say we have some sample data, here randomly generated.

julia

data = rand(nlon,nlat)

51×31 Matrix{Float64}:
 0.029418  0.367941   0.64714   0.839257   …  0.935238   0.560257   0.277788
 0.820938  0.697944   0.50779   0.15199       0.961451   0.918084   0.0502995
 0.489698  0.27281    0.115931  0.139738      0.610231   0.353555   0.130618
 0.871813  0.192756   0.326306  0.310784      0.583338   0.502005   0.745154
 0.836762  0.227963   0.922785  0.980716      0.78771    0.96868    0.979578
 0.347247  0.516954   0.756114  0.188019   …  0.0701902  0.495431   0.733122
 0.984027  0.768582   0.760056  0.0902628     0.468173   0.966308   0.489762
 0.523561  0.285832   0.898094  0.0458389     0.72295    0.98821    0.633906
 0.177707  0.48935    0.639031  0.0272078     0.447932   0.0681834  0.0323323
 0.327812  0.870306   0.495548  0.621424      0.806273   0.880876   0.939786
 ⋮                                         ⋱                        ⋮
 0.4506    0.699729   0.553912  0.66221       0.974253   0.666263   0.304148
 0.372447  0.0416205  0.842518  0.993849      0.923908   0.754426   0.730227
 0.749796  0.242462   0.773346  0.383461      0.275728   0.187629   0.85763
 0.098655  0.56095    0.613623  0.741643   …  0.443784   0.533009   0.866473
 0.741915  0.116785   0.466987  0.745438      0.600938   0.358324   0.264485
 0.773197  0.149112   0.267603  0.653191      0.344061   0.208045   0.699405
 0.237748  0.191002   0.761633  0.716134      0.436662   0.172242   0.827665
 0.564872  0.650977   0.104779  0.374332      0.754807   0.212037   0.552017
 0.888282  0.123513   0.940654  0.22069    …  0.55729    0.251782   0.886582

We extract the valid data within the GeoRegion of interest that we defined above:

julia

ndata = extract(data,ggrd)

37×17 Matrix{Float64}:
   0.691442  NaN         NaN          …  NaN         NaN  NaN  NaN  NaN
   0.965401  NaN         NaN             NaN         NaN  NaN  NaN  NaN
   0.986757    0.967179  NaN             NaN         NaN  NaN  NaN  NaN
 NaN           0.916492    0.955855      NaN         NaN  NaN  NaN  NaN
 NaN           0.172088    0.91084       NaN         NaN  NaN  NaN  NaN
 NaN           0.889395    0.228892   …  NaN         NaN  NaN  NaN  NaN
 NaN           0.862115    0.0138858     NaN         NaN  NaN  NaN  NaN
 NaN           0.428734    0.198664      NaN         NaN  NaN  NaN  NaN
 NaN         NaN           0.512622      NaN         NaN  NaN  NaN  NaN
 NaN         NaN           0.470728      NaN         NaN  NaN  NaN  NaN
   ⋮                                  ⋱                          ⋮  
 NaN         NaN         NaN               0.226804  NaN  NaN  NaN  NaN
 NaN         NaN         NaN               0.605733  NaN  NaN  NaN  NaN
 NaN         NaN         NaN          …  NaN         NaN  NaN  NaN  NaN
 NaN         NaN         NaN             NaN         NaN  NaN  NaN  NaN
 NaN         NaN         NaN             NaN         NaN  NaN  NaN  NaN
 NaN         NaN         NaN             NaN         NaN  NaN  NaN  NaN
 NaN         NaN         NaN             NaN         NaN  NaN  NaN  NaN
 NaN         NaN         NaN          …  NaN         NaN  NaN  NaN  NaN
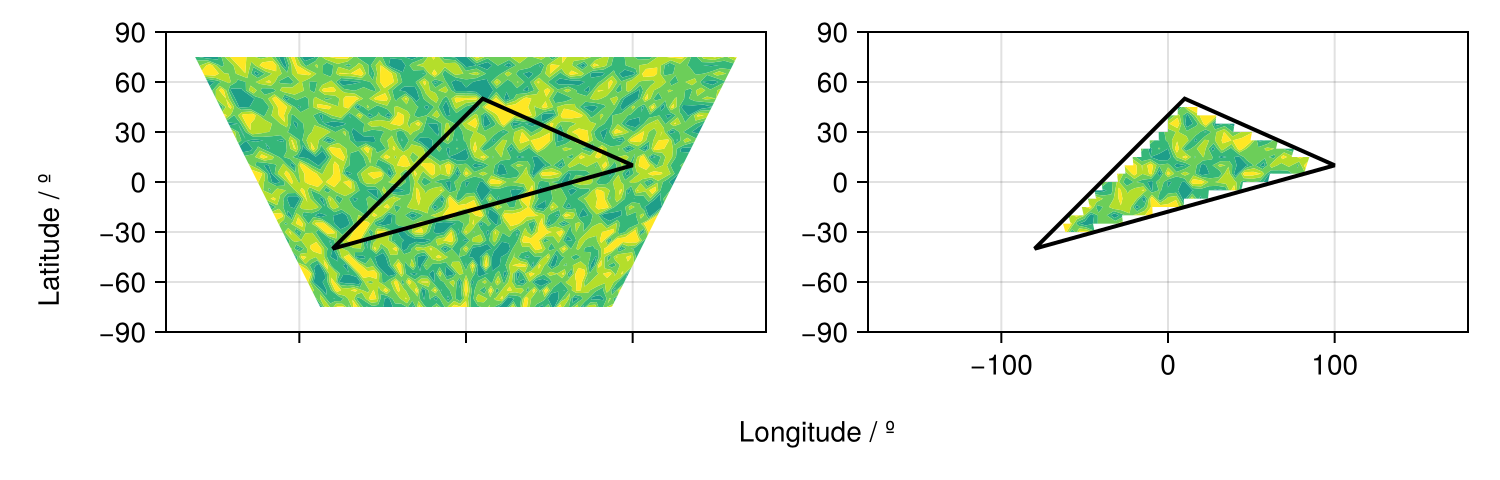
 NaN         NaN         NaN             NaN         NaN  NaN  NaN  NaN

And now let us visualize the results.

julia

slon,slat = coordinates(geo) # extract the coordinates
fig = Figure()

ax1 = Axis(
    fig[1,1],width=300,height=150,
    limits=(-180,180,-90,90)
)
contourf!(ax1,lon,lat,data,levels=-1:0.2:1)
lines!(ax1,slon,slat,color=:black,linewidth=2)
lines!(ax1,slon.+360,slat,color=:black,linewidth=2,linestyle=:dash)

hidexdecorations!(ax1,ticks=false,grid=false)

ax2 = Axis(
    fig[1,2],width=300,height=150,
    limits=(-180,180,-90,90)
)
contourf!(ax2,ggrd.lon,ggrd.lat,ndata,levels=-1:0.2:1)
lines!(ax2,slon,slat,color=:black,linewidth=2)

Label(fig[2,:],"Longitude / º")
Label(fig[:,0],"Latitude / º",rotation=pi/2)

resize_to_layout!(fig)
fig

Generalized Grids for Data Extraction ​

Creating Generalized Grids ​

What is in a Generalized Grid? ​

An example of using Generalized Grids ​

Generalized Grids for Data Extraction

Creating Generalized Grids

What is in a Generalized Grid?

An example of using Generalized Grids