RegionGrids.jl

Appearance

Unstructured Grids for Data Extraction ​

There are also RegionGrid types without an actual grid, maybe there are a set of coordinates and geometries that define the corners or the centres of a mesh, such as:

Basically, for each of these datasets, the data is given in such a way that the coordinates of the grid can be expressed via:

  • A Vector of Point2 types, with each Point2 type containing (lon,lat)
julia
using GeoRegions
using RegionGrids
using CairoMakie

Creating Unstructured Grids ​

A Unstructured Grid can be created as follows:

ggrd = RegionGrid(geo,Point2.(lon,lat))

where geo is a GeoRegion of interest that is found within the domain defined by the longitude and latitude grid vectors.

julia
lon = collect(10:20:360); nlon = length(lon)
lat = collect(-80:20:90); nlat = length(lat)

glon = zeros(nlon,nlat); glon .= lon;  glon = glon[:]
glat = zeros(nlon,nlat); glat .= lat'; glat = glat[:]

plon = glon .+ 14rand(nlon*nlat) .- 7
plat = glat .+ 14rand(nlon*nlat) .- 7

geo = GeoRegion([10,100,-80,10],[50,10,-40,50])

iggrd = RegionGrid(geo,Point2.(glon,glat))
pggrd = RegionGrid(geo,Point2.(plon,plat))
The VectorMask Grid type has the following properties:
    Indices             (ipoint) : [70, 71, 73, 74, 89, 90, 91, 92, 93, 94, 108, 109]
    Longitude Points       (lon) : [-45.34307655667226, -36.77876709238751, 16.300715051773935, 27.140990278062965, -31.101564896462378, -11.900811333392994, 16.170649910309834, 23.643136174094188, 53.817125009318445, 74.87879312706845, -4.533605078450307, 10.384761114582073]
    Latitude Points        (lat) : [-20.418087077696008, -15.88712532473336, 3.6409350931376494, 2.0581211352587996, -0.07520706019646362, 6.0719428622373925, 16.296267073610878, 26.01989307767802, 13.234261758522521, 17.64158636983985, 24.527264283725454, 34.76597950091516]
    Rotated X Coordinates    (X)
    Rotated Y Coordinates    (Y)
    Rotation (°)             (θ) : 0.0
    RegionGrid Weights (weights)
    RegionGrid Size 			  : (12,) points

The API for creating a Unstructured Grid can be found here

What is in a Unstructured Grid? ​

RegionGrids.UnstructuredGrid Type
julia
UnstructuredGrid <: RegionGrid

A UnstructuredGrid is a RegionGrid that is created based on an unstructured grid often used in cubed-sphere or unstructured-mesh grids.

All UnstructuredGrid type will contain the following fields:

  • lon - A Vector of Floats, defining the longitudes for each point in the RegionGrid that describe the region.

  • lat - A Vector of Floats, defining the latitude for each point in the RegionGrid that describe the region.

  • ipoint - A Vector of Ints, defining the indices of the valid points from the original unstructured grid that were extracted into the RegionGrid.

  • weights - A Vector of Floats, defining the latitude-weights of each valid point in the grid. Will be NaN if outside the bounds of the GeoRegion used to define this RectilinearGrid.

  • X - A Vector of Floats, defining the X-coordinates (in meters) of each point in the "derotated" RegionGrid about the centroid for the shape of the GeoRegion.

  • Y - A Vector of Floats, defining the Y-coordinates (in meters) of each point in the "derotated" RegionGrid about the centroid for the shape of the GeoRegion.

  • θ - A Float storing the information on the angle (in degrees) about which the data was rotated in the anti-clockwise direction. Mathematically, it is rotation - geo.θ.

source

We see that in a UnstructuredGrid type, we have the lon and lat vectors that defined the longitude and latitude points that are within the GeoRegion.

@example
ggrd.lon
@example
ggrd.lat

An example of using Unstructured Grids ​

Say we have some sample data, here randomly generated.

julia
data = rand(nlon,nlat)[:]
162-element Vector{Float64}:
 0.21312057522925842
 0.6800326962507157
 0.43407134407142245
 0.025933254333968536
 0.676470701150551
 0.4578902879765151
 0.9621453905370656
 0.3249231790620096
 0.3163746337516481
 0.2549750700831279
 ⋮
 0.8317888337429427
 0.6320400593375758
 0.22120888589882992
 0.1669278443669009
 0.8794258933745993
 0.48408382743659684
 0.01509470529196466
 0.3189816977880584
 0.13296466355021386

We extract the valid data within the GeoRegion of interest that we defined above:

julia
ndata = extract(data,iggrd)
pdata = extract(data,pggrd)
12-element Vector{Float64}:
 0.6835266403893645
 0.19962648634209257
 0.7515520344336604
 0.5378624142662117
 0.838261297872362
 0.1482140109754707
 0.6406531374951079
 0.9753354387320468
 0.7218324287917494
 0.4392853911888741
 0.0770502206696152
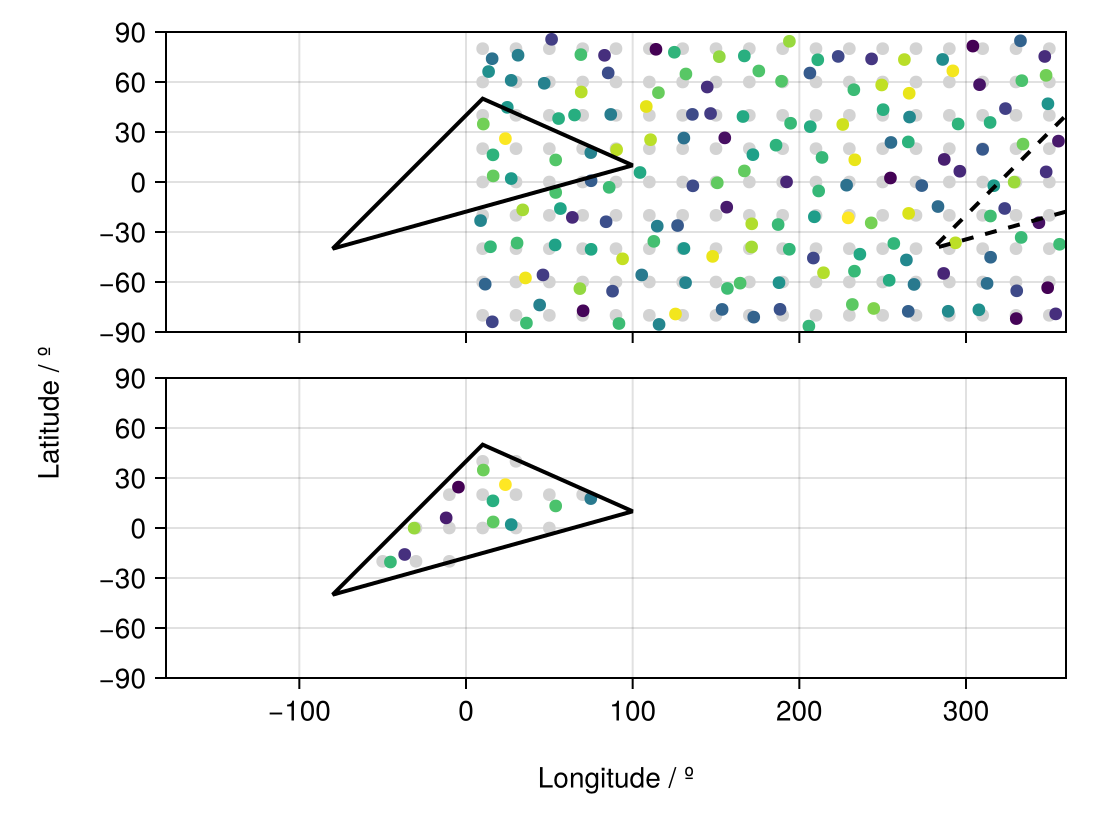
 0.7750688546815884

And now let us visualize the results.

julia
slon,slat = coordinates(geo) # extract the coordinates
fig = Figure()

ax1 = Axis(
    fig[1,1],width=450,height=150,
    limits=(-180,360,-90,90)
)
scatter!(ax1,glon,glat,color=:lightgrey)
scatter!(ax1,plon,plat,color=data)
lines!(ax1,slon,slat,color=:black,linewidth=2)
lines!(ax1,slon.+360,slat,color=:black,linewidth=2,linestyle=:dash)

hidexdecorations!(ax1,ticks=false,grid=false)

ax2 = Axis(
    fig[2,1],width=450,height=150,
    limits=(-180,360,-90,90)
)
scatter!(ax2,iggrd.lon,iggrd.lat,color=:lightgrey)
scatter!(ax2,pggrd.lon,pggrd.lat,color=pdata)
lines!(ax2,slon,slat,color=:black,linewidth=2)

Label(fig[3,:],"Longitude / º")
Label(fig[:,0],"Latitude / º",rotation=pi/2)

resize_to_layout!(fig)
fig